Se você já olhou para um mapa-múndi e pensou “Como a Groenlândia pode ser do tamanho da África?”, então já percebeu que algo está errado.
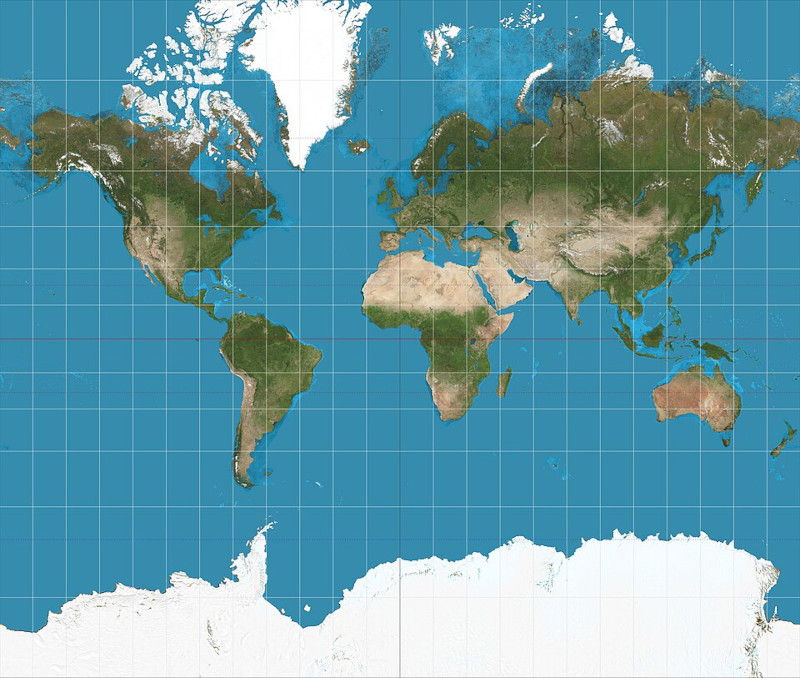
A Groenlândia não é comparável à África em tamanho, nem de longe. A África é cerca de 14 vezes maior. Ainda assim, por séculos, o mapa-múndi mais difundido sugeriu o contrário. Isso não é coincidência, erro ou simples curiosidade. É o resultado de uma projeção cartográfica específica, a chamada projeção de Mercator, e suas consequências vão muito além da cartografia.
A Impossível Tarefa de Fazer Mapas
A Terra é (aproximadamente) uma esfera. Mapas são planos. Transformar uma coisa na outra é matematicamente impossível sem distorção. Toda projeção cartográfica precisa escolher o que preservar e o que sacrificar.
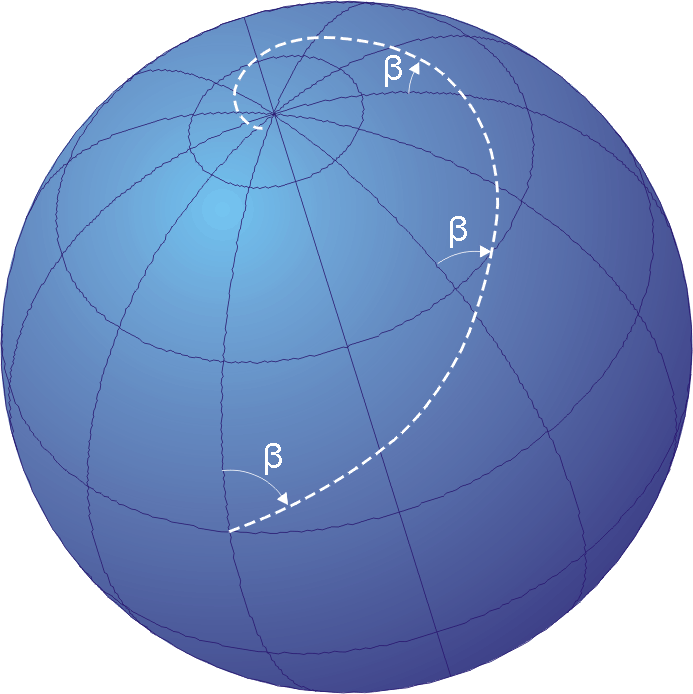
A projeção de Mercator, apresentada em 1569 por Gerardus Mercator, fez uma escolha muito clara: preservar ângulos e direções. Para navegadores em mar aberto, isso foi revolucionário. Uma linha reta em um mapa de Mercator corresponde a um rumo constante na bússola. Na era das grandes navegações, isso salvou vidas. Mas preservar direções tem um custo.
O Custo: Distorção de Área em Grande Escala
Para manter os ângulos corretos, a projeção de Mercator estica o espaço verticalmente à medida que nos afastamos do equador. Quanto maior a latitude, maior a distorção. Nos polos, essa distorção se torna infinita, e por isso eles nunca aparecem nos mapas de Mercator “verdadeiros”, originais.
Isso significa que as regiões próximas ao equador são representadas de forma relativamente fiel. Mas regiões de altas latitudes são enormemente ampliadas.
Groenlândia, Europa do Norte, Rússia, Canadá, tudo cresce desproporcionalmente. África, América do Sul, Sudeste Asiático – onde vive a maior parte da humanidade – ficam visualmente comprimidos. A matemática é neutra. O efeito, não.
Groenlândia vs. África: Uma Mentira Visual que Aprendemos Cedo
Vejamos os números:
- África: ~30,4 milhões de km²
- Groenlândia: ~2,16 milhões de km²
Em mapas de Mercator, elas parecem comparáveis. Na realidade, a África poderia conter a Groenlândia mais de uma dúzia de vezes.
Quando crianças e jovens crescem vendo a África representada como “pequena” e a Europa como “grande”, é plausível que eles internalizem uma noção distorcida do tamanho relativo das nações no cenário global muito antes de aprenderem geopolítica, economia ou história. Mapas treinam silenciosamente a intuição, e a intuição orienta o julgamento.
Poder, Percepção e Imaginação Política
É aqui que a cartografia se torna política. Quando a África é sistematicamente mostrada como pequena, isso convida, ainda que de forma sutil, ao desprezo. Um continente que parece reduzido no papel é mais fácil de imaginar como marginal, subdesenvolvido ou dispensável. Quando a Groenlândia aparece gigantesca, vazia, branca, dominante, ela desperta fantasias estratégicas, disputas por recursos e até ideias de conquista. Isso não acontece porque mapas causam imperialismo ou conflitos. Acontece porque eles moldam o cenário mental no qual decisões políticas são tomadas.
Líderes mal informados não começam com más intenções; começam com intuições equivocadas. Se a imagem mental do mundo exagera o tamanho e a centralidade do Norte Global e minimiza o Sul Global, decisões sobre intervenção, negligência, extração ou “interesse estratégico” já nascem enviesadas, antes mesmo da leitura do primeiro relatório de inteligência.
Ninguém em 1569 criou a projeção de Mercator para servir ao poder colonial. Mas continuar a colocá-la no centro da educação, da mídia e das instituições hoje já não é mais inocente.
Distorção como Amplificador
É importante ser claro: a projeção de Mercator não é a raiz dos conflitos humanos. Mas ela atua como um amplificador de equívocos. Ela reforça uma hierarquia visual: o que é grande parece importante; o que é pequeno parece descartável; o que está na periferia se torna ignorável.
Ao longo dos séculos, essa hierarquia coincidiu de forma desconfortável com a história da colonização, da exploração e das desigualdades globais. Quando combinada com ignorância, nacionalismo ou ambição, a geografia distorcida se torna mais um fator que normaliza o tratamento desigual de povos e territórios. Por certo mapas não determinam políticas, mas fazem certas políticas parecerem mais “naturais” do que outras.
Destronar Mercator
No mundo contemporâneo, a justificativa original da projeção de Mercator praticamente desapareceu. Não navegamos mais traçando rumos em mapas pendurados na parede; GPS e sistemas digitais substituíram cartas náuticas; Hoje, precisamos mais de noções corretas de escala, população e equilíbrio global do que de linhas de rumo.
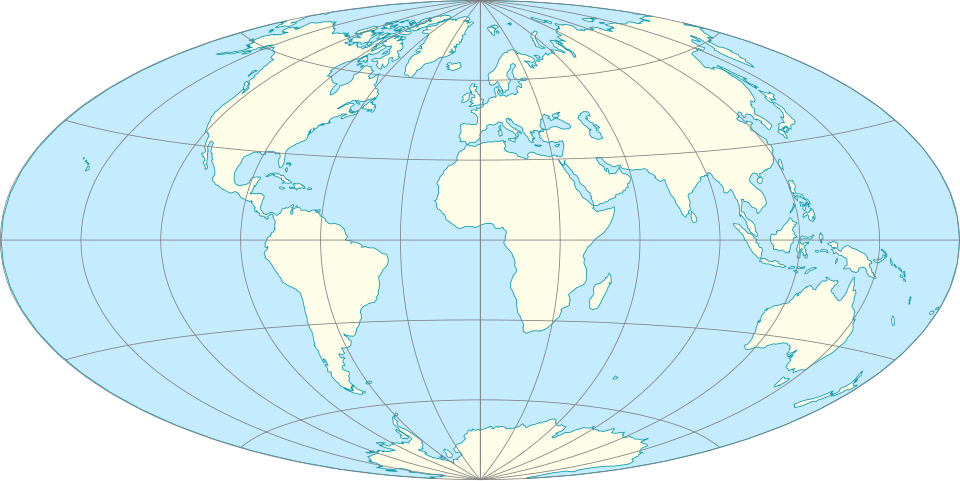
Existem muitas alternativas; projeções de área equivalente ou de compromisso, que oferecem uma visão muito mais honesta do planeta. Nenhuma é perfeita. Mas várias são menos enganosas. Manter Mercator como o mapa-padrão apenas reflete um hábito cultural; não é uma necessidade técnica.
Convite a Uma Visão Mais Honesta
Adotar projeções mais realistas não vai resolver a injustiça global nem acabar com guerras. Mas elimina uma distorção persistente na forma como imaginamos o planeta e nosso lugar nele. Não precisamos de mapas que privilegiem conveniências do século XVI. Precisamos de mapas que reflitam o mundo como ele realmente é: vasto, desigual, interconectado e compartilhado.
A projeção de Mercator cumpriu seu papel. O mundo mudou. Apegarmo-nos a ela hoje não preserva a tradição; preserva, sim, a distorção. Se queremos menos ilusões sobre poder, tamanho e importância, devemos começar corrigindo a imagem na parede. Mapas moldam mentes e mentes, cedo ou tarde, moldam a história.